前不久，有幸聆听了我校特级教师、校长吴明富对“问题解决策略”的点评，他毋庸置疑地指出画图策略在问题解决方法中有着举足轻重的分量，在教学中默默彰显其魅力，不禁让我联想到自己的想法和吴校长不谋而合，现结合自身教学，浅谈本人的几点思考：
 　 一、画图帮助学生在理解题意时拨开云雾
 　 如教学苏教版六年级下册第6页第四题：
  　2005年，我国公布了新的个人所得税征收标准。个人月收入1600元以下不征税。月收入超过1600元，超过部分按下面的标准征税。
  　不超过500元的 5%
 　 超过500元～2000元的部分 10%
 　 超过2000元～5000元的部分 15%
  　李明的妈妈月收入1800元，爸爸月收入2500元，他们各应缴纳个人所得税多少元？
 　 学生刚拿到此题，不知所云，对什么是“超过部分”、“不超过部分”，以及“超过部分”按区域进行征税这些说法，如果只靠教师单纯的文字解释，恐怕很难让学生准确无误地求出爸爸应缴纳的个人所得税，所以教学中我想是否可以用画图来表达题目的意思，沿着这样的思路往下思考，最后得出以下的示意图：
  1600元基准线

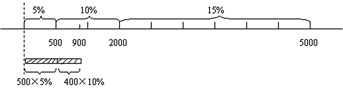
  将1600元作为基准线，超过的部分按题意分成四段：不超过500元为一段、500元～2000元为一段、2000元～5000元为一段，5000元以上为一段。爸爸月收入超过基准部分应为：2500－1600=900（元），“900元”横跨图形中的两段，即其中的500元按（500×5%）征税，其余的400元应按（400×10%）征税。边看示意图边解释边做，学生一目了然。如再追加一问：爸爸月收入4500元该如何征税？学生列出：（500×5%+1500×10%+900×15%）元，说明他们真的弄懂了。
 　 二、画图帮助学生在解决问题过程中茅塞顿开
 　 线段图是画图当中最常见的图形，一提到线段图，人们首先想到的就是“和倍”、“差倍”问题，而我最切身地体验却是在教学苏教版五年级下册89页练一练中：小军收集了一些画片，他拿出画片的一半还多一张送给小明，自己还剩25张。小军原来有多少张画片？记得当初第一次讲完例题让学生们做，待他们做完后，我巡视一周，发现全班只有两个学生答案是正确的，学生的错误算式都是：25×2+1=51（张）。由于错误率太高，所以当时记忆很深刻，究其原因，原来学生对“画片的一半还多一张”还不能真正明白，于是，我便提示让他们用线段图来画一画，帮助理解题意。大多数孩子在我的提示下画出了题目的雏形，稍作修改后板演在黑板上：

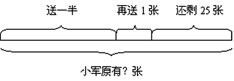
  当线段图完整地出现在黑板上时，我轻轻地问了一句：你能找到画片的另一半在哪儿了吗？学生们立刻明白了：画片的一半应是（25+1）张。用（25+1）×2=52（张）才是正确答案。再试着让学生根据题目整理出条件：
  　原有？张画片→送一半画片→再送1张→还剩25张
  　结合刚才的图形找一找当初的想法为什么错了，错在哪儿。当第二轮再次教到此内容时，我已做到心中有数了。回想这一段，我认为当学生身陷困境、百思不得其解时，线段图的适时介入恰是“善解人意”的关怀和帮助，触及了学生的精神需要——寻求“突围”，发挥了线段图的高效作用，所以对学生来说是“我画因我需”，而对我们来说则应是“生需故我画”。
  　三、画图帮助学生在形成概念过程中入木三分
  　“认识比”是苏教版六年级上册内容，教学例题时，我将主题图换成了线段图，图形如下：
  　果汁：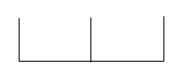
  　牛奶：
  　替换成图形后，引导学生把具体的“杯数”改成“份数”，让学生隐隐发现“比”不仅可以表示两个具体数量之间的关系，还可以表示两个“份数”之间的关系，为后面正确理解倍比关系的两个量奠定坚实的基础。学生在画线段图的过程中，首先要考虑用一定长度的线段代表一杯的数量，这样果汁应画成两份，牛奶应画成三份，然后得出果汁与牛奶的数量比是2∶3，学生经历了从具体数量到抽象份数的过程，拓宽了思维的广度，为后续理解比的意义做好了充分的准备，也让“比”的概念在学生的脑海中逐步清晰了起来。
  　图是思维过程的表征方式，“图”能让学生看见“关系”、找到“门路”，它能帮助学生理解题意、构建概念、协助分析、理清过程。如何使学生进一步体会画图的价值，并且在需要时自觉想到运用画图策略，并能通过画图有效解决问题，仍是我在今后的教学中需要不断思考的问题，我将为此而努力。